- Esercitatore: Dr. Carmelo Finocchiaro
Studio N. 201
Ricevimento Studenti: Lunedì 13-15 oppure per appuntamento da fissare per email
carmelo(at)mat.uniroma3.it
__________________________________
I Settimana (19-23 Settembre)
Le esercitazioni iniziano a partire dalla II settimana di lezione.
__________________________________
Le esercitazioni iniziano a partire dalla II settimana di lezione.
__________________________________
II Settimana (26-30 Settembre)
Introduzione: il metodo di studio per seguire con profitto Algebra I.
Un'introduzione storica alla Teoria degli Insiemi: l'approccio "ingenuo" di Cantor.
Il paradosso di Russell, suo superamento con il sistema di Zermelo-Fraenkel (cenni a qualche utile assioma), insiemi e classi proprie. Assioma di esistenza dell'insieme vuoto.
Logica, connettivi, tavole di verità. Uguaglianze e inclusioni insiemistiche, esempi e controesempi. Insiemi transitivi. Unione e intersezione fra insiemi.
__________________________________
VI Settimana (24-28 Ottobre)
Esempi di relazioni di equivalenza e insiemi quoziente. Maggioranti, minoranti, estremo superiore e estremo inferiore in insiemi ordinati. Esercizi di ricapitolazione.
Radici n-esime di un numero complesso, radici n-esime dell'unità, esempi.
Esempi di corrispondenze e funzioni, controimmagini di insiemi, funzioni iniettive (e non) e suriettive (e non). Caratterizzazioni di iniettività e suriettività di una funzione in termini delle sue fibre. Biiezioni ed equipotenza fra insiemi, numerabilità. Esistono parti proprie di un insieme infinito X che sono equipotenti a X.
Una bigezione esplicita fra N e Z, e fra N e N x N . Procedimento diagonale di Cantor. Il Teorema fondamentale delle funzioni e suo uso. Una biiezione fra S^1 (la circonferenza) e un insieme-quoziente della retta reale.
Descrizione dell'insieme-quoziente Q / Z.
__________________________________
__________________________________
__________________________________
XI Settimana (4-9 Dicembre)
Sottogruppi di un gruppo ciclico finito e loro ordine, esempi. Laterali associati a un sottogruppo di un gruppo, proprietà ed esempi. Teorema di Lagrange e sua dimostrazione (e un esempio che illustra l'idea della dimostrazione), esempi e applicazioni: ogni gruppo finito con p elementi (p primo) è ciclico, una prova alternativa del Teorema di Eulero-Fermat. Ogni gruppo nel quale il quadrato di ogni elemento è banale è abeliano. Classificazione dei gruppi ciclici, a meno di isomorfismi. Classificazione dei gruppi con 4 elementi, a meno di isomorfismi. Applicazioni del Teorema dell'Omomorfismo. Un isomorfismo fra i gruppi U(Z/rsZ) e U(Z/rZ) x U(Z/sZ), con MCD(r, s)=1. Omomorfismi di Z/4Z in S_3 e omomorfismi di S_3 in Z/4Z.
__________________________________
XII Settimana (11-16 Dicembre)
Osservazioni su laterali, quozienti ed esempi. Dato un sottogruppo H di un gruppo, G allora gH = H se e soltanto se g è elemento di H. Se G è un gruppo finito con n elementi e H è normale in G e ha d elementi, allora G/H ha n/d elementi. Se H è un sottogruppo di un gruppo G avente la metà degli elementi di G, allora H è normale in G. Esempi. Il gruppo alterno A_n su n elementi e sua cardinalità. Descrizione della struttura ciclica delle permutazioni di S_4. Il Teorema di Lagrange non si inverte: infatti A_4 non ha sottogruppi con 6 elementi. Svolgimento di esercizi per casa.
Esempi di anelli e sottoanelli. Descrizione del sottoanello Z[i \sqrt 6] di C e calcolo dei suoi elementi invertibili. La cosiddetta "localizzazione di Z in 2" Z_(2) (i.e. l'insieme dei numeri razionali aventi una espressione con denominatore dispari) è un sottoanello di Q. Calcolo degli elementi invertibili di Z_(2). Particolari sottoanelli dell'anello delle funzioni A^X delle funzioni da un insieme non vuoto X in un anello A. L'anello delle funzioni a valori reali che sono limitate. L'anello dei polinomi a valori interi è un sottoanello di Q[T] contenente propriamente Z[T].
__________________________________
XIII Settimana (18-21 Dicembre)
Classificazione dei polinomi irriducibili a coefficienti reali. Esercizi di ricapitolazione su anelli, sottoanelli, ideali, divisori dello zero e invertibili, svolgimento di un esercizio assegnato nella seconda prova in itinere dello scorso anno. Richiami su anelli quoziente. Un quoziente di un anello di polinomi K[T] su un campo K, rispetto all'ideale generato da un polinomio f, è un campo se e solo se f è irriducibile in K[T]. Come calcolare l'inverso della classe di un polinomio in un quoziente del tipo K[T] /fK[T] .
Esempi di campi finiti, costruzione esplicita di un campo con 9 elementi. Esercizio per casa: si esibisca un campo con 25 elementi.
Un un polinomio f su un campo K è irriducibile se e soltanto se esso è primo. Classificazione dei divisori dello zero in un quoziente di un anello di polinomi su un campo rispetto a un ideale generato dal prodotto di due polinomi irriducibili, esempi. Applicazioni del Teorema Fondamentale dell'Omomorfismo tra anelli.
Per ogni anello (commutativo con unità) A, il quoziente A[T]/TA[T] è isomorfo a A.
Z[T]/nZ[T] è isomorfo a (Z/nZ)[T]. Z[T]/(n,T)Z[T] è isomorfo a Z/nZ.
Costruzione esplicita del più piccolo sottocampo di C nel quale il polinomio T^2+1 ha radici.
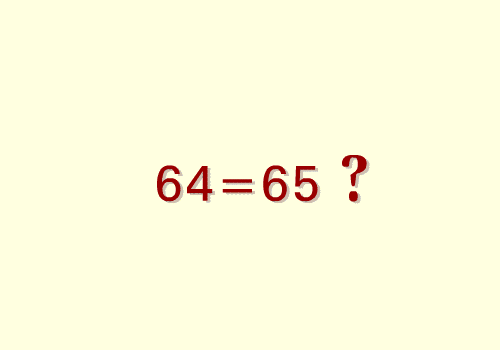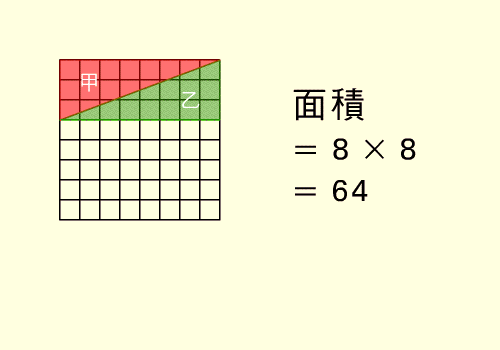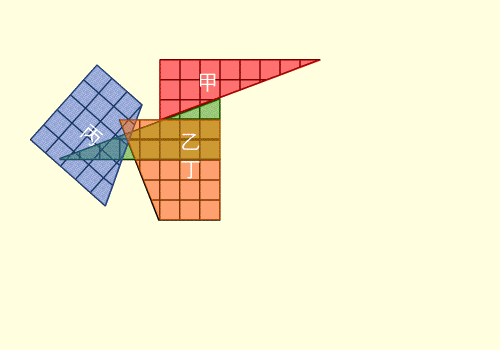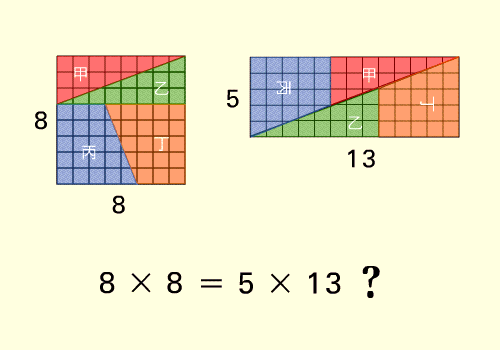
Introduzione: il metodo di studio per seguire con profitto Algebra I.
Un'introduzione storica alla Teoria degli Insiemi: l'approccio "ingenuo" di Cantor.
Il paradosso di Russell, suo superamento con il sistema di Zermelo-Fraenkel (cenni a qualche utile assioma), insiemi e classi proprie. Assioma di esistenza dell'insieme vuoto.
Logica, connettivi, tavole di verità. Uguaglianze e inclusioni insiemistiche, esempi e controesempi. Insiemi transitivi. Unione e intersezione fra insiemi.
__________________________________
III Settimana (3-7 Ottobre)
Applicazioni dei Principi di Induzione e Ampia Induzione, e dimostrazione dell'equivalenza di questi enunciati. Un esempio per illustrare come applicare il Principio di Induzione in modo poco rigoroso genera paradossi. Progressioni aritmetiche, Successioni definite per ricorrenza, Numeri di Fibonacci, coefficienti binomiali e binomio di Newton.
__________________________________
__________________________________Applicazioni dei Principi di Induzione e Ampia Induzione, e dimostrazione dell'equivalenza di questi enunciati. Un esempio per illustrare come applicare il Principio di Induzione in modo poco rigoroso genera paradossi. Progressioni aritmetiche, Successioni definite per ricorrenza, Numeri di Fibonacci, coefficienti binomiali e binomio di Newton.
__________________________________
IV Settimana (10-14 Ottobre), Esercitatore Dott. Antonio Cigliola
__________________________________
V Settimana (17-21 Ottobre)
Il problema della ricerca di tutte le identità di Bézout di un MCD motiva lo studio delle equazioni diofantee lineari. Criterio di risolubilità di un'equazione diofantea lineare in due indeterminate. Algoritmo per risolvere tali equazioni diofantee. Esercizi sulla nozione di numero primo e sul Teorema fondamentale dell'Aritmetica. Ordini su un insieme, massimi e minimi, elementi massimali e minimali. Insiemi bene ordinati, esempi ed esercizi. VI Settimana (24-28 Ottobre)
Esempi di relazioni di equivalenza e insiemi quoziente. Maggioranti, minoranti, estremo superiore e estremo inferiore in insiemi ordinati. Esercizi di ricapitolazione.
Radici n-esime di un numero complesso, radici n-esime dell'unità, esempi.
__________________________________
VII Settimana (7-10 Novembre)
Svolgimento degli esercizi sul Principio di Induzione apparsi nella prima prova in itinere. Equazioni lineari in una indeterminata in Z/nZ, criterio di risolubilità, esempi. Invertibili in Z/nZ ed esempi. L'inverso di un elemento di Z/nZ, se esiste, è unico. L'indicatore di Eulero, teorema di moltiplicatività dell'indicatore di Eulero e sue applicazioni per determinare \varphi(n), per ogni intero positivo. Il Teorema Cinese dei Resti, sua dimostrazione ed esempi. Come ricondurre, quando possibile, un generico sistema di congruenze lineari in una incognita in forma normale. Applicazioni del Teorema di Eulero.
__________________________________
VIII Settimana (14-17 Novembre)
Una bigezione esplicita fra N e Z, e fra N e N x N . Procedimento diagonale di Cantor. Il Teorema fondamentale delle funzioni e suo uso. Una biiezione fra S^1 (la circonferenza) e un insieme-quoziente della retta reale.
Descrizione dell'insieme-quoziente Q / Z.
__________________________________
IX Settimana (21-24 Novembre)
Il Teorema del doppio quoziente e sue applicazioni. Varie caratterizzazioni di un insieme infinito. Confronto di cardinalità. Biiezioni di un insieme in sé. Esempi di biiezioni che non commutano in ogni insieme con almeno 3 elementi. Supporto di una biiezione di un insieme in sé e sue proprietà, biiezioni con supporti disgiunti commutano. Permutazioni, k-cicli e trasposizioni. Ogni permutazione si decompone nella composizione di cicli disgiunti. Ogni ciclo è composizione di trasposizioni. Segno di una permutazione e sue proprietà. __________________________________
X Settimana (28-30 Novembre)
Commenti sull'Assioma della Scelta e suo uso per dimostrare che, dati due insiemi A e B esiste un'applicazione iniettiva da A in B se e soltanto se esiste un'applicazione surgettiva da B in A. Numerabilità dell'insieme dei numeri razionali. Uso della densità di Q in R per dimostrare che l'insieme dei numeri reali è equipotente all'insieme delle parti di N. Per ogni insieme X, non esiste alcuna applicazione surgettiva da X in P(X). Il Teorema di Eisenstein e sue applicazioni. Condizioni sufficienti per l'irriducibilità di polinomi di grado al più 3. Come determinare eventuali radici razionali di polinomi a coefficienti interi (Teorema di Ruffini), esempi e applicazioni. Irriducibilità del p-esimo polinomio ciclotomico (con p primo). Esempi di insiemi con operazioni associative che sono commutative (o non), che hanno elemento neutro (o non), che hanno elemento neutro sinistro e/o destro (o non). Esempi non standard di gruppi. Calcolo dell'ordine di una potenza di un generatore di un gruppo ciclico finito ed esempi. Calcolo dell'ordine di un prodotto di elementi permutabili aventi ordini coprimi ed esempi. Ordine di un k-ciclo in S_n. I sottogruppi di un gruppo ciclico sono ciclici.__________________________________
XI Settimana (4-9 Dicembre)
Sottogruppi di un gruppo ciclico finito e loro ordine, esempi. Laterali associati a un sottogruppo di un gruppo, proprietà ed esempi. Teorema di Lagrange e sua dimostrazione (e un esempio che illustra l'idea della dimostrazione), esempi e applicazioni: ogni gruppo finito con p elementi (p primo) è ciclico, una prova alternativa del Teorema di Eulero-Fermat. Ogni gruppo nel quale il quadrato di ogni elemento è banale è abeliano. Classificazione dei gruppi ciclici, a meno di isomorfismi. Classificazione dei gruppi con 4 elementi, a meno di isomorfismi. Applicazioni del Teorema dell'Omomorfismo. Un isomorfismo fra i gruppi U(Z/rsZ) e U(Z/rZ) x U(Z/sZ), con MCD(r, s)=1. Omomorfismi di Z/4Z in S_3 e omomorfismi di S_3 in Z/4Z.
__________________________________
XII Settimana (11-16 Dicembre)
Osservazioni su laterali, quozienti ed esempi. Dato un sottogruppo H di un gruppo, G allora gH = H se e soltanto se g è elemento di H. Se G è un gruppo finito con n elementi e H è normale in G e ha d elementi, allora G/H ha n/d elementi. Se H è un sottogruppo di un gruppo G avente la metà degli elementi di G, allora H è normale in G. Esempi. Il gruppo alterno A_n su n elementi e sua cardinalità. Descrizione della struttura ciclica delle permutazioni di S_4. Il Teorema di Lagrange non si inverte: infatti A_4 non ha sottogruppi con 6 elementi. Svolgimento di esercizi per casa.
Esempi di anelli e sottoanelli. Descrizione del sottoanello Z[i \sqrt 6] di C e calcolo dei suoi elementi invertibili. La cosiddetta "localizzazione di Z in 2" Z_(2) (i.e. l'insieme dei numeri razionali aventi una espressione con denominatore dispari) è un sottoanello di Q. Calcolo degli elementi invertibili di Z_(2). Particolari sottoanelli dell'anello delle funzioni A^X delle funzioni da un insieme non vuoto X in un anello A. L'anello delle funzioni a valori reali che sono limitate. L'anello dei polinomi a valori interi è un sottoanello di Q[T] contenente propriamente Z[T].
__________________________________
XIII Settimana (18-21 Dicembre)
Classificazione dei polinomi irriducibili a coefficienti reali. Esercizi di ricapitolazione su anelli, sottoanelli, ideali, divisori dello zero e invertibili, svolgimento di un esercizio assegnato nella seconda prova in itinere dello scorso anno. Richiami su anelli quoziente. Un quoziente di un anello di polinomi K[T] su un campo K, rispetto all'ideale generato da un polinomio f, è un campo se e solo se f è irriducibile in K[T]. Come calcolare l'inverso della classe di un polinomio in un quoziente del tipo K[T] /fK[T] .
Esempi di campi finiti, costruzione esplicita di un campo con 9 elementi. Esercizio per casa: si esibisca un campo con 25 elementi.
Un un polinomio f su un campo K è irriducibile se e soltanto se esso è primo. Classificazione dei divisori dello zero in un quoziente di un anello di polinomi su un campo rispetto a un ideale generato dal prodotto di due polinomi irriducibili, esempi. Applicazioni del Teorema Fondamentale dell'Omomorfismo tra anelli.
Per ogni anello (commutativo con unità) A, il quoziente A[T]/TA[T] è isomorfo a A.
Z[T]/nZ[T] è isomorfo a (Z/nZ)[T]. Z[T]/(n,T)Z[T] è isomorfo a Z/nZ.
Costruzione esplicita del più piccolo sottocampo di C nel quale il polinomio T^2+1 ha radici.
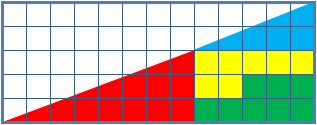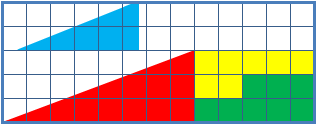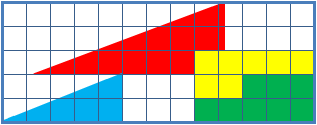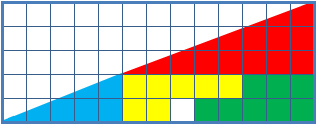
Alcune ..... pseudo-dimostrazioni
(trovare gli errori)
Il quadratino .... perduto

64 = 65 ??
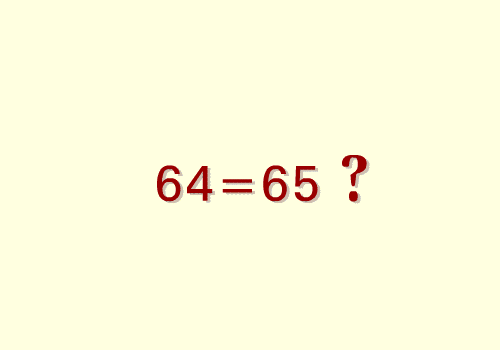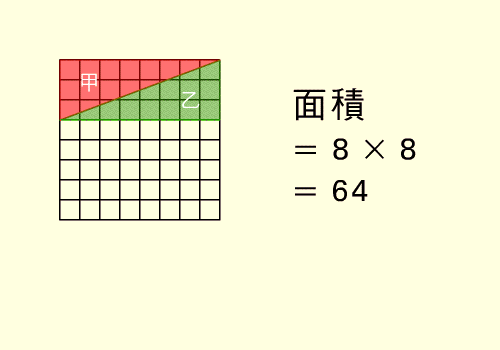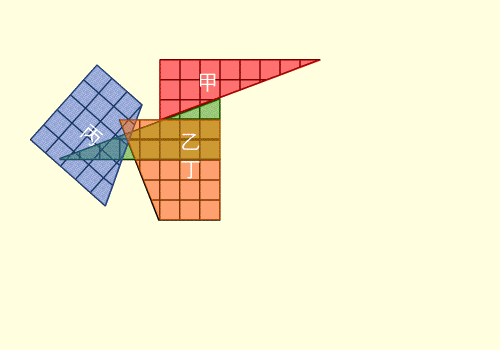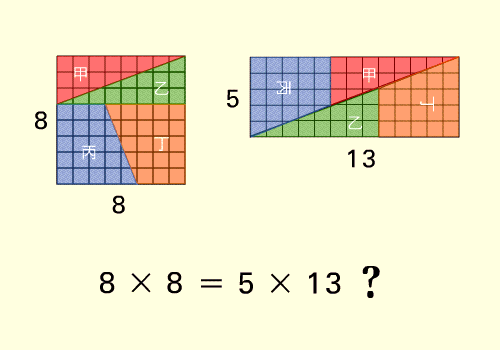
Aiuto sto impazzendo!
RispondiElimina